Unsupervised Learning - Deep Generative Model

参考链接：

https://www.bilibili.com/video/BV1Wv411h7kN?p=65&vd_source=909d7728ce838d2b9656fb13a31483ca

https://www.bilibili.com/video/BV1Wv411h7kN?p=66&spm_id_from=pageDriver&vd_source=909d7728ce838d2b9656fb13a31483ca

Theory behind VAE

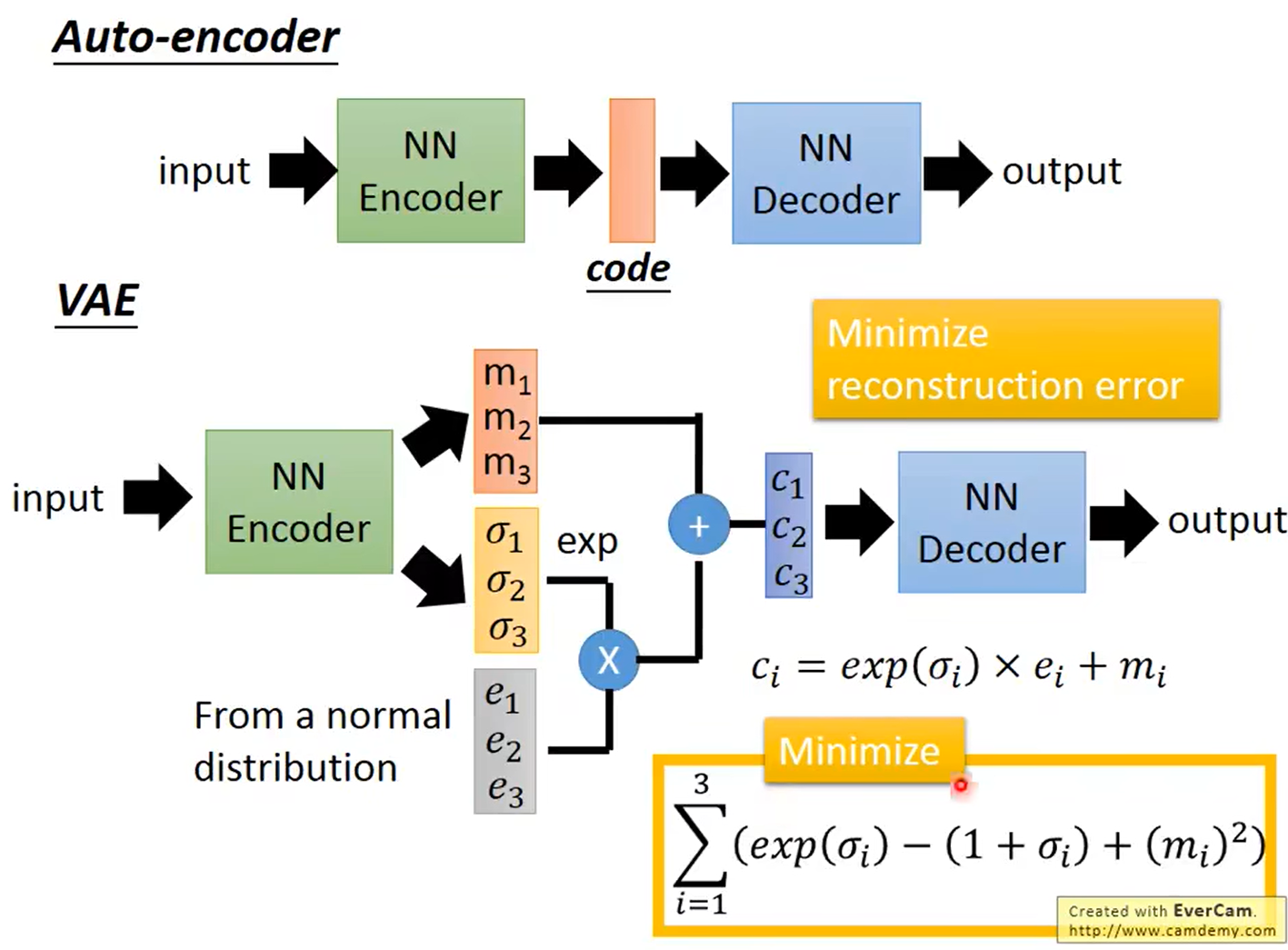
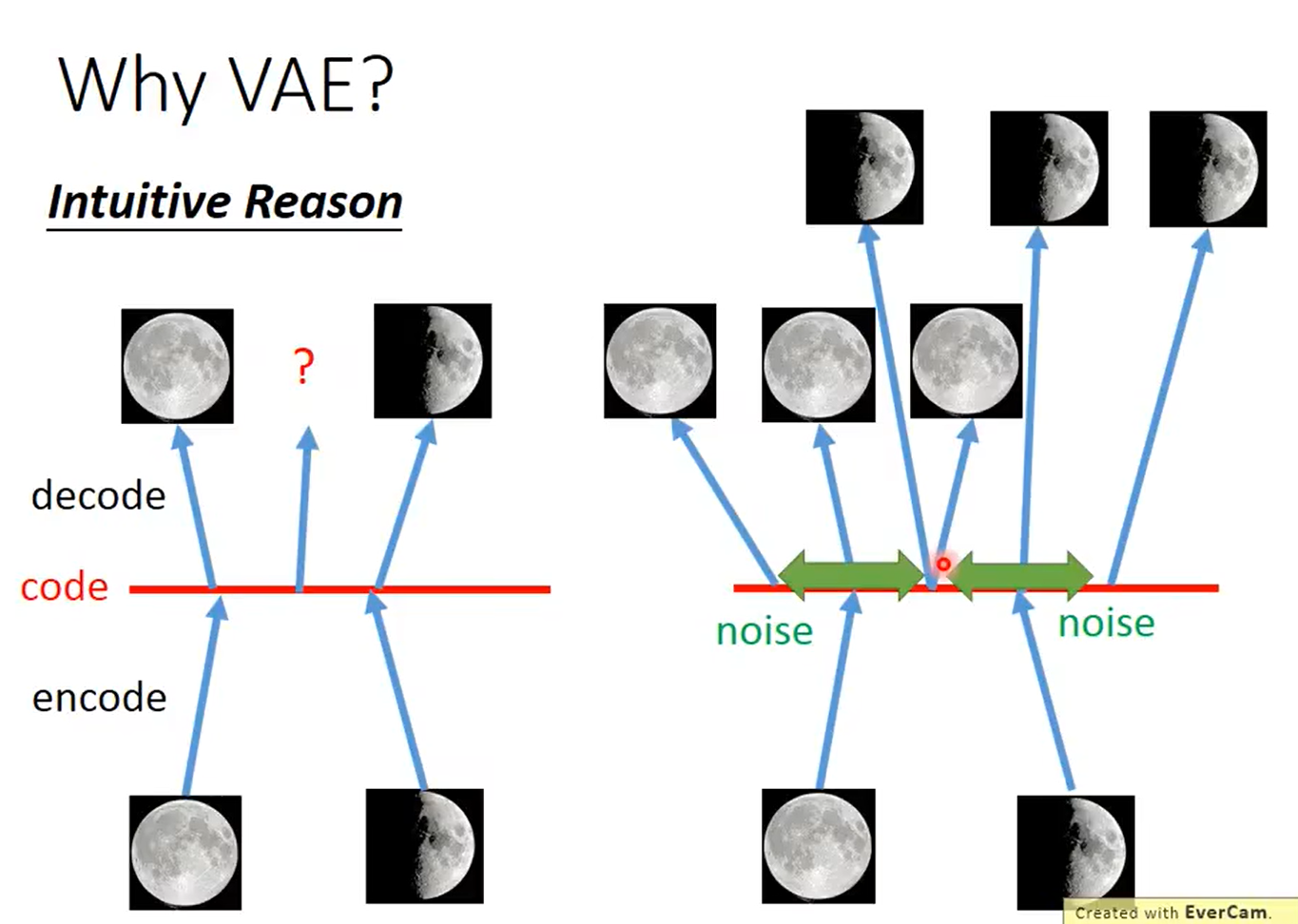
提出VAE的直觉：

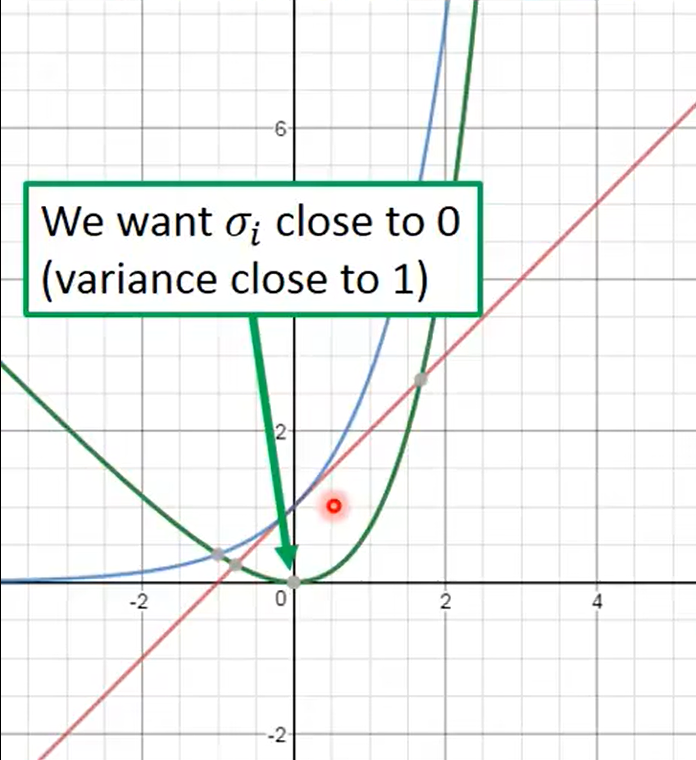
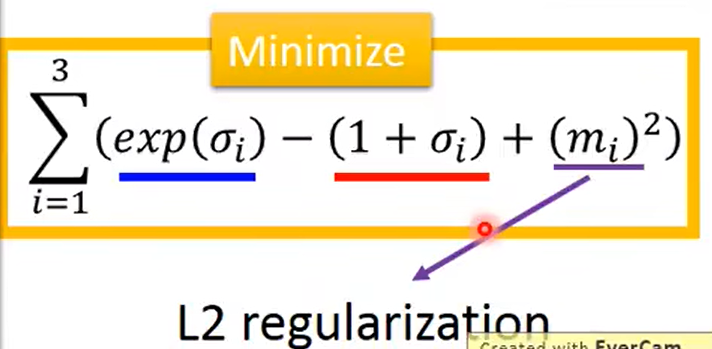
若使$\sum_{i=1}^3{\left( e^{\sigma _i}-\left( 1+\sigma _i \right) +\left( m_i \right) ^2 \right)}$最小化，则$\sigma _i$应该趋近于0，则方差$e^{\sigma _i}$趋近于1。$m_i$为均值，$m_i$趋近于0，故q(z|x)趋近于均值为0，方差为1的分布。由于对于任一个X，所有的 p(Z|X) 都很接近标准正态分布 N(0,I)。也就是下面这个推导：

这样我们就能达到我们的先验假设：p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。

上面这个式子在博客下半部分也提到了。这里再放一篇博客，有利于理解VAE：https://blog.csdn.net/a312863063/article/details/87953517

总结

However, we’re trying to build a generative model here, not just a fuzzy data structure that can “memorize” images. We can’t generate anything yet, since we don’t know how to create latent vectors other than encoding them from images.

There’s a simple solution here. We add a constraint on the encoding network, that forces it to generate latent vectors that roughly follow a unit gaussian distribution. It is this constraint that separates a variational autoencoder from a standard one.

Generating new images is now easy: all we need to do is sample a latent vector from the unit gaussian and pass it into the decoder.

We let the network decide this itself. For our loss term, we sum up two separate losses: the generative loss, which is a mean squared error that measures how accurately the network reconstructed the images, and a latent loss, which is the KL divergence that measures how closely the latent variables match a unit gaussian.

1
2
3
generation_loss = mean(square(generated_image - real_image))
latent_loss = KL-Divergence(latent_variable, unit_gaussian)
loss = generation_loss + latent_loss

In order to optimize the KL divergence, we need to apply a simple reparameterization trick: instead of the encoder generating a vector of real values, it will generate a vector of means and a vector of standard deviations.

A downside to the VAE is that it uses direct mean squared error instead of an adversarial network, so the network tends to produce more blurry images.

There’s been some work looking into combining the VAE and the GAN: Using the same encoder-decoder setup, but using an adversarial network as a metric for training the decoder.

Problems of VAE

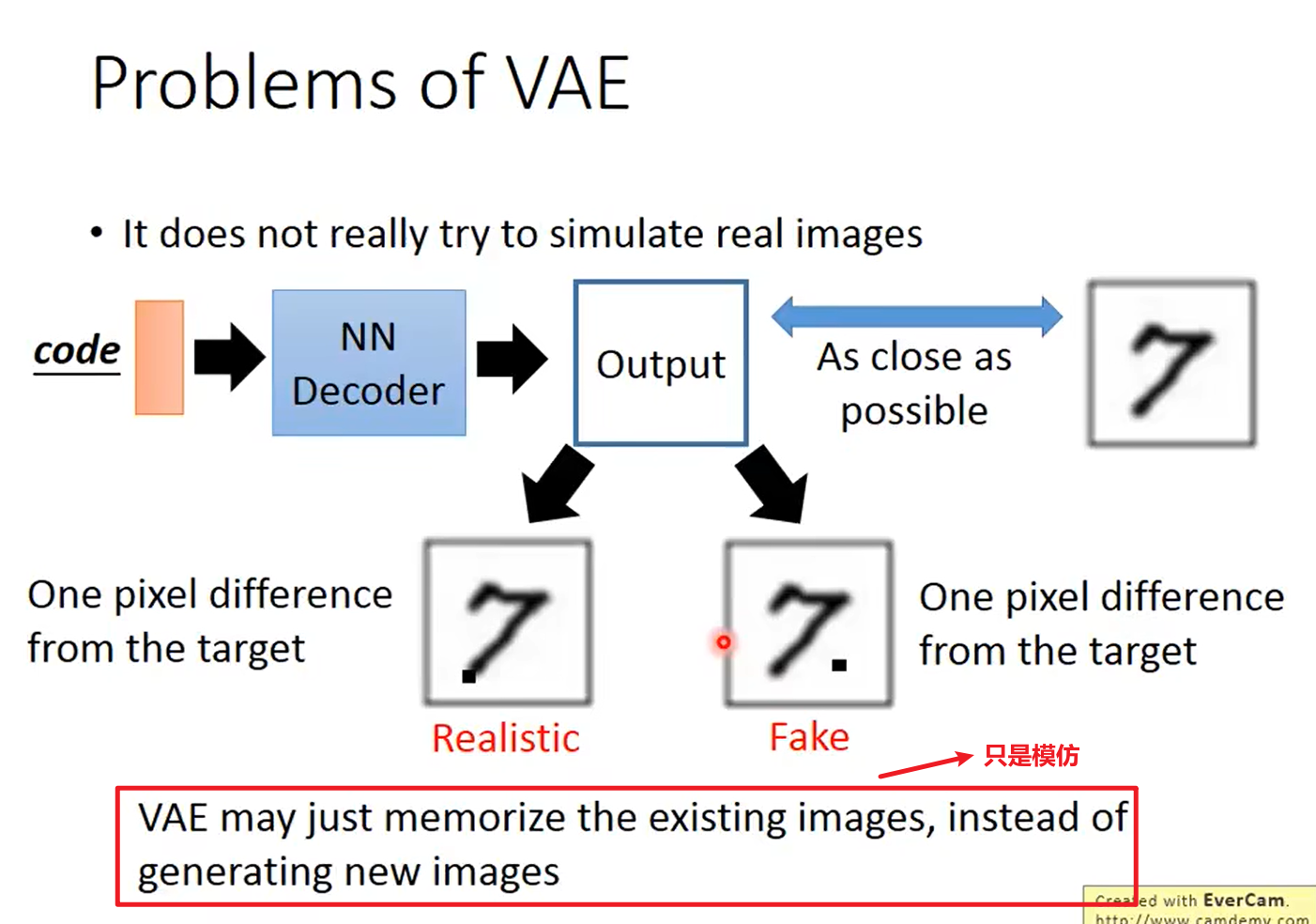
博客

https://lilianweng.github.io/posts/2018-08-12-vae/

https://zhuanlan.zhihu.com/p/34998569

https://kvfrans.com/variational-autoencoders-explained/

https://spaces.ac.cn/archives/5343

https://spaces.ac.cn/archives/7725

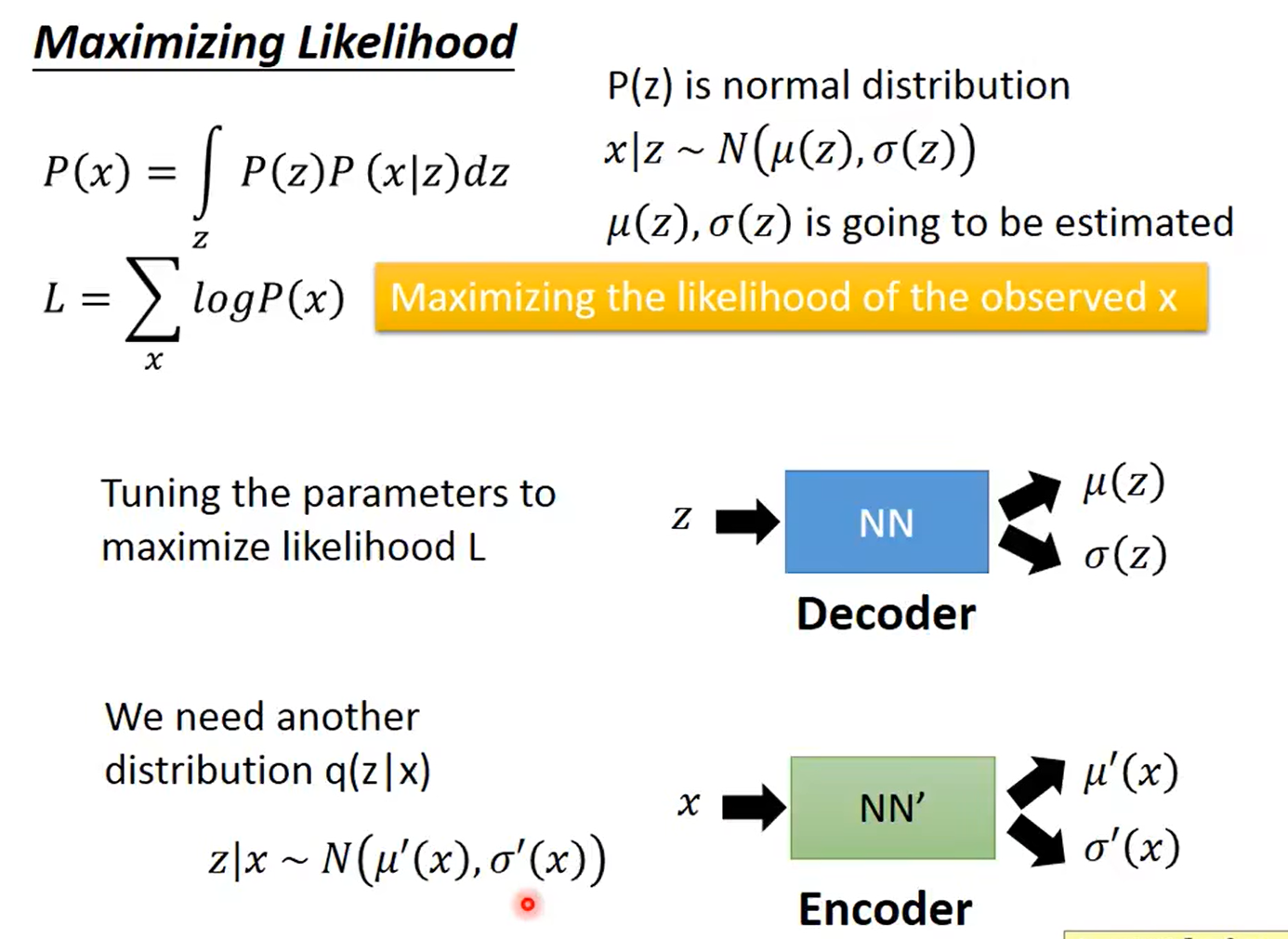
那我怎么找出专属于 $X_k$ 的正态分布 p(Z|$X_k$) 的均值和方差呢？好像并没有什么直接的思路。

那好吧，我就用神经网络来拟合出来。这就是神经网络时代的哲学：难算的我们都用神经网络来拟合，在 WGAN 那里我们已经体验过一次了，现在再次体验到了。

于是我们构建两个神经网络 $μ_k$=f1($X_k$)，log$σ^2$=f2($X_k$) 来算它们了。我们选择拟合 log$σ^2$ 而不是直接拟合 $σ^2$，是因为 $σ^2$ 总是非负的，需要加激活函数处理，而拟合 log$σ^2$ 不需要加激活函数，因为它可正可负。

到这里，我能知道专属于 $X_k$ 的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个 $Z_k$ 出来，然后经过一个生成器得到 $\hat{X}_k$=g($Z_k$)。

现在我们可以放心地最小化 $D(\hat{X}_k,X_k)^2$，因为 $Z_k$ 是从专属 $X_k$ 的分布中采样出来的，这个生成器应该要把开始的 $X_k$ 还原回来。

VAE 是为每个样本构造专属的正态分布，然后采样来重构。

其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。

这样我们就能达到我们的先验假设：p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。

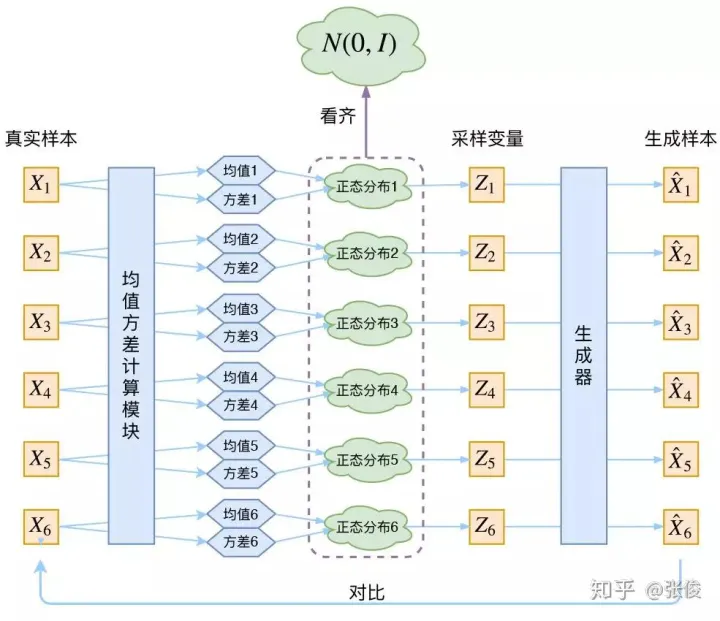
怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢？

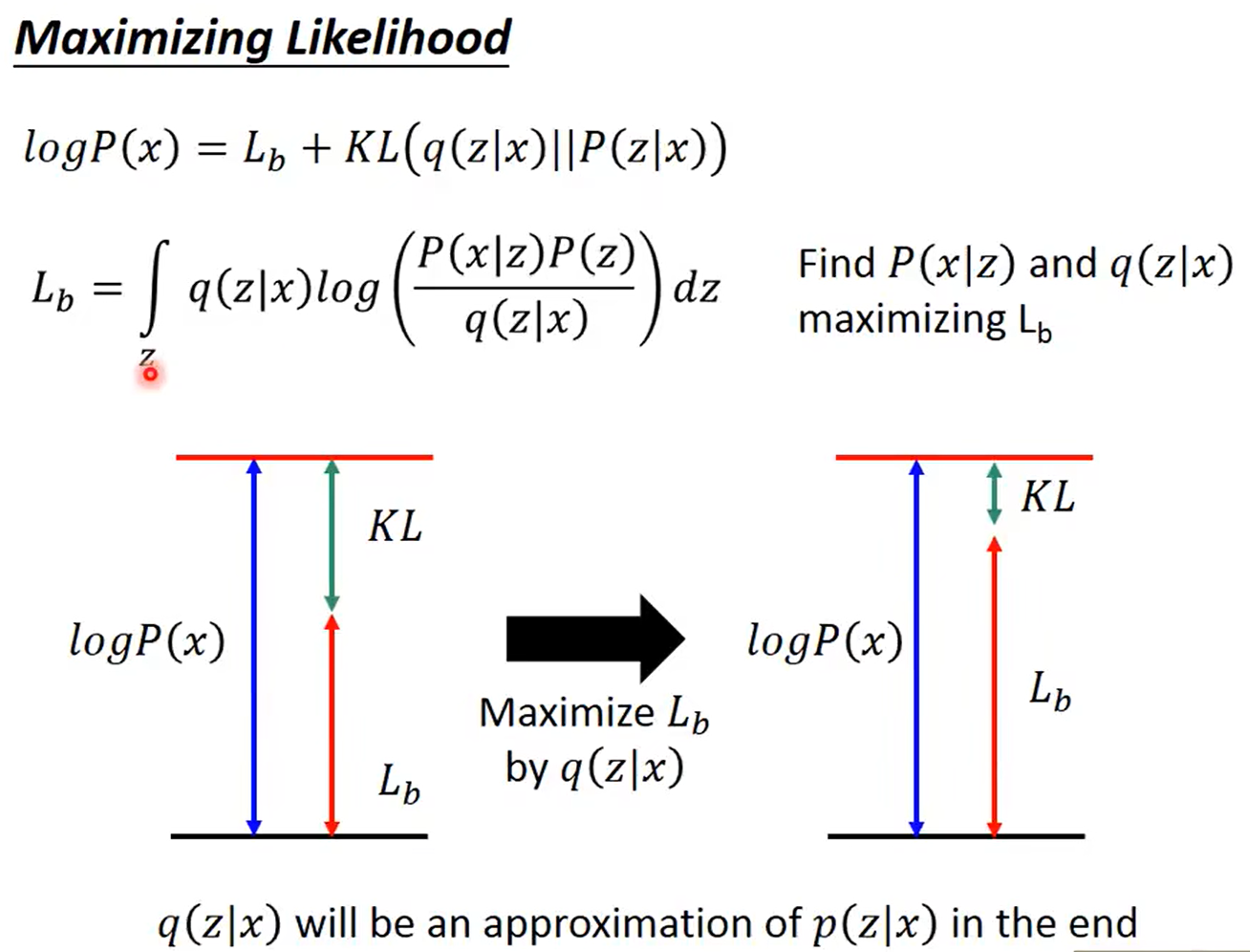
原论文直接算了一般（各分量独立的）正态分布与标准正态分布的 KL 散度KL(N(μ,$σ^2$)‖N(0,I))作为这个额外的 loss，计算结果为：

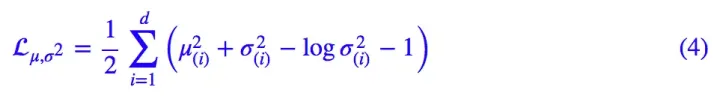
重参数技巧

最后是实现模型的一个技巧，英文名是 Reparameterization Trick，我这里叫它做重参数吧。

就是我们要从 p(Z|$X_k$) 中采样一个 $Z_k$ 出来，尽管我们知道了 p(Z|$X_k$) 是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的，于是我们利用了一个事实：

所以，我们将从 N(μ,$σ^2$) 采样变成了从 N(0,$1$) 中采样，然后通过参数变换得到从N(μ,$σ^2$) 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

中间插入一部分，这段为个人理解：

如何进行采样操作？如下图。输入任意一个样本$X_k$，这个$X_k$对应的分布p(z|$X_k$)的均值为$\mu _k$，方差为$e^{\sigma _k}$。从分布均值为$\mu _k$，方差为$e^{\sigma _k}$的分布中进行采样这个操作，通过换一种方式进行，即先从N(0,I)中采样个$\varepsilon$，然后$z\,\,=\,\,\mu _k\,\,+\,\,\varepsilon \times e^{\sigma _k}$ ，也就实现了采样这个操作，后来随着训练进行，均值为$\mu _k$，方差$e^{\sigma _k}$都趋近于0。p(z|$X_k$)在最大化$-KL(q(z|x)||P(z))$的操作下与$P(z)$接近，且$q(z|x)$的均值趋近于0，方差趋近于1，因此$P(z)$的均值趋近于0，方差趋近于1，也符合一开始“假设服从标准的正态分布，那么我就可以从中采样得到若干个 Z1,Z2,…,Zn，然后对它做变换得到 X̂1=g(Z1),X̂2=g(Z2),…,X̂n=g(Zn)”这个假设。

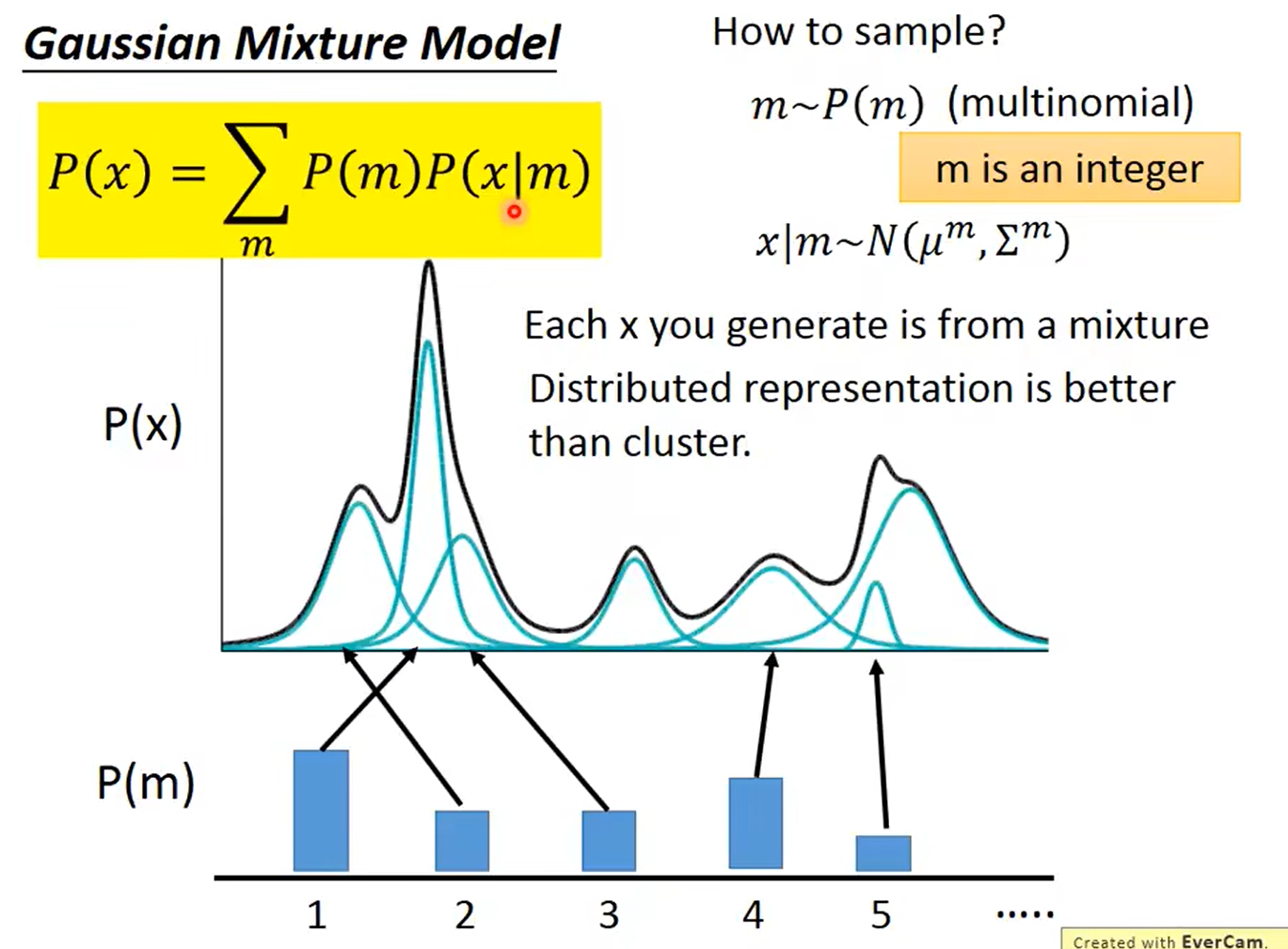
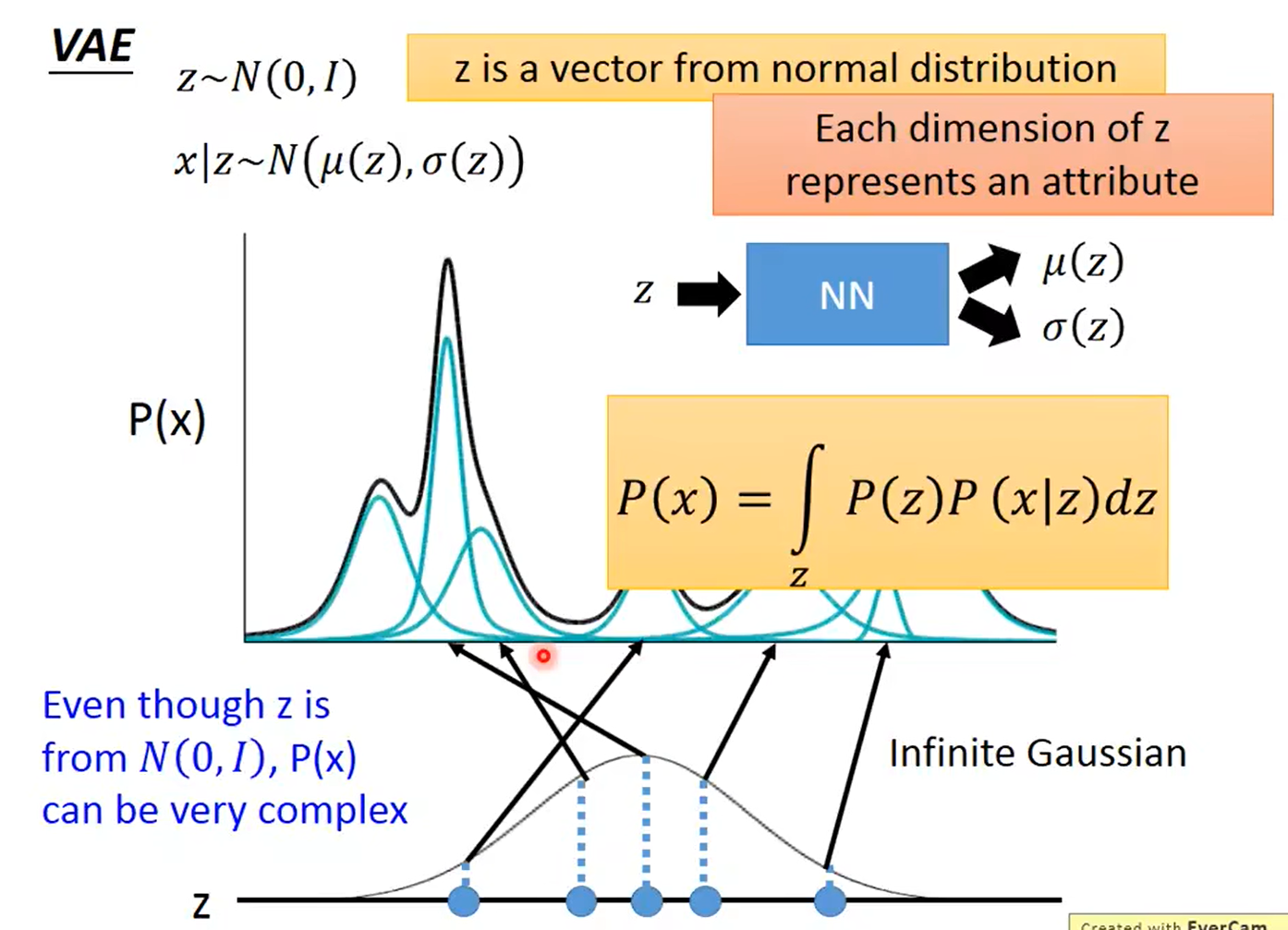
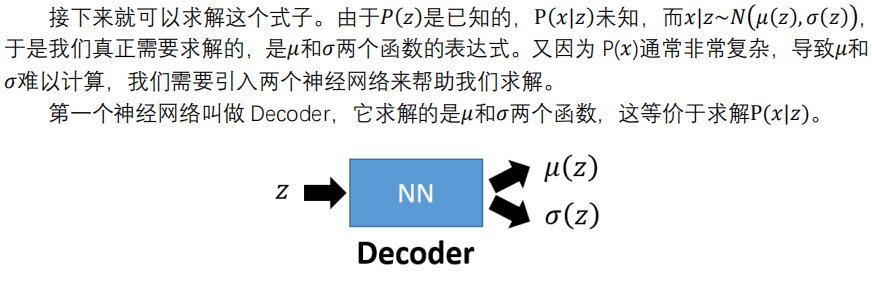
而p(z|$X_k$)的引入，是为了辅助求解P(x|z)，而P(z)是标准正态分布，故进而可以最大化$P\left( x \right) \,\,=\,\,\int\limits_z{P\left( z \right) P\left( x|z \right) dz}$。P(x|z)这一部分是decoder，不断调整P(x|z)使P(x)最大，其中蕴含了高斯混合模型的思想。如下图：

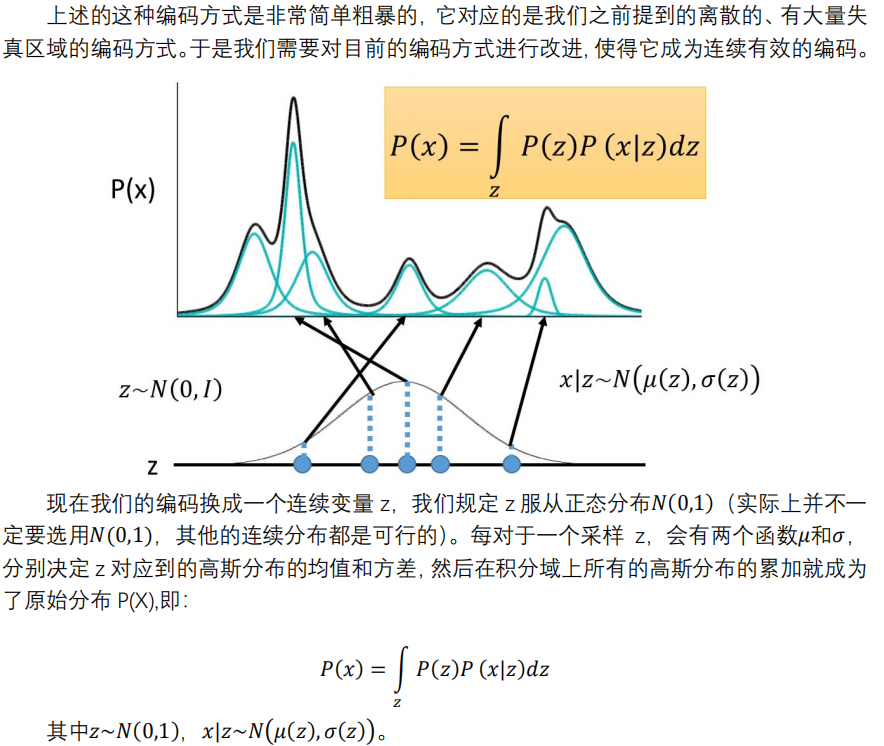
事实上，我觉得 VAE 从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的。

它本质上就是在我们常规的自编码器的基础上，对 encoder 的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果 decoder 能够对噪声有鲁棒性；而那个额外的 KL loss（目的是让均值为 0，方差为 1），事实上就是相当于对 encoder 的一个正则项，希望 encoder 出来的东西均有零均值。

那另外一个 encoder（对应着计算方差的网络）的作用呢？它是用来动态调节噪声的强度的。

直觉上来想，当 decoder 还没有训练好时（重构误差远大于 KL loss），就会适当降低噪声（KL loss 增加），使得拟合起来容易一些（重构误差开始下降）。

反之，如果 decoder 训练得还不错时（重构误差小于 KL loss），这时候噪声就会增加（KL loss 减少），使得拟合更加困难了（重构误差又开始增加），这时候 decoder 就要想办法提高它的生成能力了。

pytorch代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
import torch
from torch.autograd import Variable
import numpy as np
import torch.nn.functional as F
import torchvision
from torchvision import transforms
import torch.optim as optim
from torch import nn
import matplotlib.pyplot as plt
from torch import distributions

class Encoder(torch.nn.Module):
    def __init__(self, D_in, H, latent_size):
        super(Encoder, self).__init__()
        self.linear1 = torch.nn.Linear(D_in, H)
        self.linear2 = torch.nn.Linear(H, H)
        self.enc_mu = torch.nn.Linear(H, latent_size)
        self.enc_log_sigma = torch.nn.Linear(H, latent_size)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        mu = self.enc_mu(x)
        log_sigma = self.enc_log_sigma(x)
        sigma = torch.exp(log_sigma)
        return torch.distributions.Normal(loc=mu, scale=sigma)


class Decoder(torch.nn.Module):
    def __init__(self, D_in, H, D_out):
        super(Decoder, self).__init__()
        self.linear1 = torch.nn.Linear(D_in, H)
        self.linear2 = torch.nn.Linear(H, D_out)
        

    def forward(self, x):
        x = F.relu(self.linear1(x))
        mu = torch.tanh(self.linear2(x))
        return torch.distributions.Normal(mu, torch.ones_like(mu))

class VAE(torch.nn.Module):
    def __init__(self, encoder, decoder):
        super(VAE, self).__init__()
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, state):
        q_z = self.encoder(state)
        z = q_z.rsample()      #rsample()不是在定义的正太分布上采样，而是先对标准正太分布N(0,1)进行采样，然后输出:mean+std×采样值
        return self.decoder(z), q_z


transform = transforms.Compose(
    [transforms.ToTensor(),
     # Normalize the images to be -0.5, 0.5
     transforms.Normalize(0.5, 1)]
    )
mnist = torchvision.datasets.MNIST('./', download=True, transform=transform)

input_dim = 28 * 28
batch_size = 128
num_epochs = 100
learning_rate = 0.001
hidden_size = 512
latent_size = 8

if torch.cuda.is_available():
    device = torch.device('cuda')
else:
    device = torch.device('cpu')

dataloader = torch.utils.data.DataLoader(
    mnist, batch_size=batch_size,
    shuffle=True, 
    pin_memory=torch.cuda.is_available())

print('Number of samples: ', len(mnist))

encoder = Encoder(input_dim, hidden_size, latent_size)
decoder = Decoder(latent_size, hidden_size, input_dim)

vae = VAE(encoder, decoder).to(device)

optimizer = optim.Adam(vae.parameters(), lr=learning_rate)
for epoch in range(num_epochs):
    for data in dataloader:
        inputs, _ = data
        inputs = inputs.view(-1, input_dim).to(device)
        optimizer.zero_grad()
        p_x, q_z = vae(inputs)
        log_likelihood = p_x.log_prob(inputs).sum(-1).mean()    #logprob = dist.log_prob(sample) means to get the logarithmic probability (logprob) of one experiment sample (sample) under a specific distribution (dist).
        kl = torch.distributions.kl_divergence(                 #Log probability: https://en.wikipedia.org/wiki/Log_probability
            q_z, 
            torch.distributions.Normal(0, 1.)
        ).sum(-1).mean()
        loss = -(log_likelihood - kl)
        loss.backward()
        optimizer.step()
        l = loss.item()
    print(epoch, l, log_likelihood.item(), kl.item())

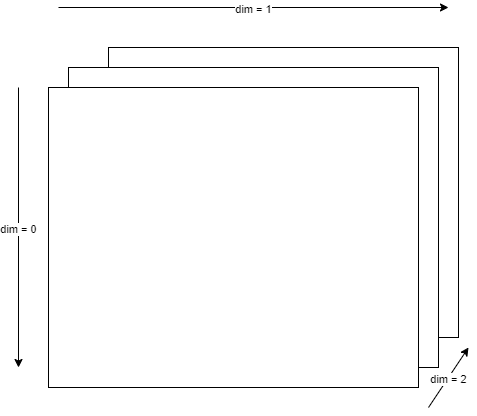
A tensor has multiple dimensions, ordered as in the following figure. There is a forward and backward indexing. Forward indexing uses positive integers, backward indexing uses negative integers.

Example:

-1 will be the last one, in our case it will be dim=2

-2 will be dim=1

-3 will be dim=0

CVAE

https://agustinus.kristia.de/techblog/2016/12/17/conditional-vae/

VAE-GAN

http://www.twistedwg.com/2018/01/31/VAE+GAN.html

VQ-VAE

https://spaces.ac.cn/archives/6760

为什么$p(z)$得是标准正态分布呢？

其实不一定，因为这个是先验分布，人为定义的。

https://aitechtogether.com/article/8412.html